
みなさんこんにちは! 林です。

早稲田大学中退。楽器を弾くことと都市伝説が好き。アイリッシュテナーバンジョーという素朴な音色の民族楽器を改造して、パンクロックを演奏するおそらく日本で唯一の人物。最近は水タバコにはまっている。
以前「ダジャレーヌちゃん 世界のたび」Twitterプロモーションキャンペーンに絡めてオカルトを交えつつ、確率に関する記事を書きました。

キャンペーンへの応募は夜だと当たりやすい?
ただしオカルトです
意外と好評だったようで、僕は味を占めました(!?)ので、今回も確率に関する記事です。
古今東西、数学クイズや論理パズルなどで確率の問題は数多く存在しますが、理系の方も文系の方も関係なく、確率っておもしろいんだぜ! と思えるような問題を紹介していこうと思います。
直感では信じがたい、不思議な確率の問題を集めました! すぐに答えを見てしまうのではなく、ぜひ少し自分で考えてみてからお楽しみください。
子供の性別を当ててみて

Aさんには二人の子供がいます。あなたがAさんにお子さんの性別を尋ねたところ、Aさんは「一人は男の子ですよ。」と答えました。この時もう一人の子供の性別が、男の子である確率と女の子である確率はそれぞれどれくらいでしょうか?
なおこの二人は双子ではなく、男の子が生まれる確率と女の子が生まれる確率は50%ずつとします。
一見すると、兄弟がいようがいまいが子供の性別には全く関係ないから確率は50%ずつのように思えますが・・・
少し下にスクロールすると答えがあります。
答え
「もう一人の子供が女の子である確率は2/3(約66%)、男の子である確率は1/3(約33%)」
どうしてこうなるのか解説していきましょう。
まず二人の子供がいる時の、性別のパターンを以下に並べます。
- 上が男の子、下も男の子
- 上が男の子、下が女の子
- 上が女の子、下が男の子
- 上が女の子、下も女の子
この4通りになりますね。1~4の確率は全て同じです。しかしAさんの情報から一人は男の子なので、「4.上が女の子、下も女の子」というパターンがありえないことがわかります。
残った三つのパターンは、
- 上が男の子、下も男の子
- 上が男の子、下が女の子
- 上が女の子、下が男の子
となります。
1~3も確率は全て同じですので、「もう一人の子供が女の子である確率は2/3(約66%)、男の子である確率は1/3(約33%)」という結果になります。
ちなみに、もしAさんが「上の子は男の子ですよ。」と答えた場合、1と2のパターンしか残らないため、確率は50%ずつになります。得られる情報によって確率が変わってしまうんですね。(そもそも初めからもったいぶらないで二人とも教えてよ、という意見は心の隅にしまっておきましょう。)
なお、この問題は数学で出てくる「条件付き確率」の説明でよく使われます。興味がある方は以下のリンク先もご覧いただければ、より一層学びが深まります。
さて、続いてもう一問見てみましょう。みんな大好き(?)スマートフォンのゲームによくある「ガチャ」に関する問題です。
「レア」が当たる確率
スマートフォンゲーム内に1%の確率で「レア」を排出するガチャがあり、あなたはそのガチャを100回引くことができます。
あなたが「(最低でも1枚以上)レアを引ける確率」はどのくらいでしょうか?
※今回の問題はスマートフォンのゲームによくある「一般的なガチャ」の場合とします。「ボックスガチャ」などと呼ばれるような特殊なガチャは今回の問題の対象にはなりません。
きちんと計算すると大変なのでなんとなくで構いません。このくらいの確率だろうとイメージしてみてください。1%ということは確率は1/100なんだから、100回引けばほぼ間違いなくレアをゲットできるだろう、そう思いますか?
少し下にスクロールすると答えがあります。
答え
「約63%」
意外と低いと感じたでしょうか。それでは解説をしていきます。
まず大前提として、レアを引く確率(当たり)が1%ということは、レア以外を引く確率(はずれ)は99%だということを確認しておきましょう。
このガチャを2回引いた時の確率を考えましょう。起こりうるパターンは以下の4通りです。
- 2回とも当たるパターン
1%×1%=0.01% - 1回目当たり、2回目はずれのパターン
1%×99%=0.99% - 1回目はずれ、2回目当たりのパターン
99%×1%=0.99% - 2回ともはずれのパターン
99%×99%=98.01%
それでは「レアを引ける確率」はいくらでしょう? リストの上3つまでのパターンが「レアが出た確率」です。全て足すと1.99%になります。
では3回引いた時の確率はいくらでしょう? まずは起こりうるパターンをすべて書き出してみます。
- 3回とも当たるパターン
- 1回目2回目に当たりが出て、3回目はずれのパターン
- 1回目3回目に当たりが出て、2回目はずれのパターン
- 2回目3回目に当たりが出て、1回目はずれのパターン
- 1回目に当たりが出て、2回目3回目はずれのパターン
- 2回目に当たりが出て、1回目3回目はずれのパターン
- 3回目に当たりが出て、1回目2回目はずれのパターン
- 3回ともはずれのパターン
3回引いただけでも、起こりうるパターンの数は8通りになるので、計算も大変になってきます。100回引いた時の計算の労力はパターンの数が膨大すぎて想像したくもありません※。
※ちなみにガチャを100回引いた時の起こりうるパターンの数は約127穣通りになります。127の後に0を28個書かなければならない、とんでもなく大きい数です・・・
ではどうやって「レアを引ける確率」を計算するか?
もう一度、ガチャを2回引いた時の確率を見てみましょう。
「レアを引ける確率」が1.99%、2回ともはずれの「レアを引けない確率」が98.01%ですので下の図のように表すことができます。

図から、「レアを引ける確率」+「レアを引けない確率」= 100%になっていることがわかります(回数が3回でも100回でもこの式は成り立ちます)。
この式を変形すると、「100%」ー「レアを引けない確率」= 「レアを引ける確率」が成り立ちます。
したがって「レアを引ける確率」を求めるには、何通りもあるパターンをわざわざ計算しなくても「レアを引けない確率」だけ計算して100%から引けば求められることがわかりました!
実際に試してみましょう。3回引いた時の「レアを引けない確率」は3回連続で外れる確率、つまり99%×99%×99%=97.03%なので、3回引いた時に「レアを引ける確率」は100%ー97.03%=2.97%となります。簡単ですね!
以上のことを踏まえて100回引いた時の確率を求めてみましょう。
100回引いてレアが出ない確率は、100回連続でハズレを引き続ける確率なので、99%×99%×99%×・・・と、99%を100回かければ求めることができます。これなら電卓でも計算できます。その計算結果は36.60%となります。
したがって100%ー36.60%=63.40%が「100回引いた時にレアを引ける確率」となります。
10人に3、4人はレアを引けずに涙を飲むこととなるんですね。
この問題を解く際に用いた式は余事象の確率というものでした。高校の数学Aの分野で習う内容(2019年現在)ですが、みなさん覚えていたでしょうか?
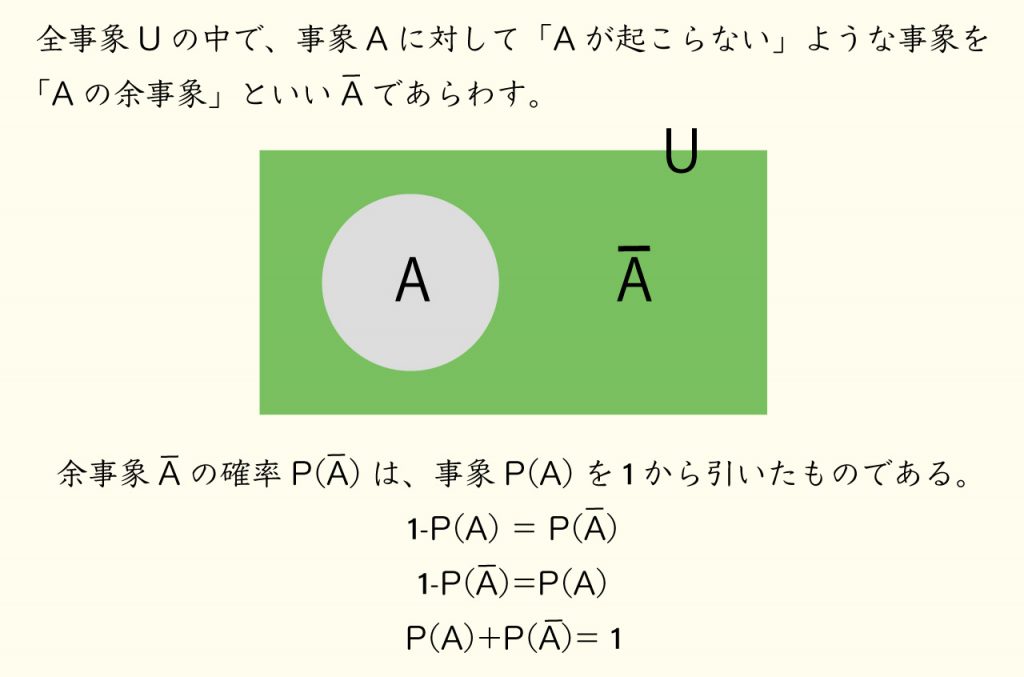
この話を語る上でかかせないのが、スマートフォンゲーム内で行われている一般的なガチャは「くじ引き」とは違うという点です。一般的なくじ引きの場合、抽選箱の中に入ってるくじの総数はくじを引くごとに減っていき、箱の中のくじがなくなるまで引きつづければ必ず当たりが出ます。(某YouTuberがお祭りのくじ屋でそれを実行して、全部引いても当たりくじが入ってなかったことが判明し話題になりましたが・・・)
しかし今回の問題に出てくるスマートフォンゲーム内のガチャの場合は、毎回ハズレくじを抽選箱の中に戻すようなもので、永遠にハズレを引き続ける可能性があるということです。
実際、当たりが1%の排出率のガチャの場合、約20人に1人は300回ガチャを引いても当たりません。1万回引いても当たらない人がいても、それは決してあり得ない話ではないのです。
スマートフォンゲームの有料のガチャをする際は、ご自分の財政状況等に合わせてほどほどに…
さて、いかがだったでしょうか。今回は自分の直感とは異なるような不思議な確率の問題を2問紹介しました。
次回もまだまだ不思議な確率問題を紹介するのでお楽しみに!






