
みなさんこんにちは! 林です。

早稲田大学中退。楽器を弾くことと都市伝説が好き。アイリッシュテナーバンジョーという素朴な音色の民族楽器を改造して、パンクロックを演奏するおそらく日本で唯一の人物。最近は粘土細工にはまっている。
303 BOOKSの母体であるオフィス303では、これまでに多くのパズル誌を製作してきました。今回は303 BOOKSの記事でもパズルを紹介していこうと思います。
頭を捻らなければ解けないような論理パズルをご紹介していきますので、ぜひ挑戦してみてください!
睡眠薬入りジュース
あなたの前にジュースの入ったビンが1,000本あります。ビンの見た目は全て同じもので見た目から区別することはできません。
この1,000本のジュースのうち、1本だけ睡眠薬が入っているジュースがあります。この睡眠薬は飲んでから1時間から2時間で効果が出ますが、いつ効果が現れるか正確な時間はわからず、人によって効き始める時間も異なります。しかしどんな人でも2時間以内には必ず眠ってしまいます。
あなたはどのジュースに睡眠薬が入っているのかを2時間以内に確実に特定しなければならず、そのためにジュースを飲んでくれる人を集めることになりました。さて、睡眠薬入りジュースを確実に特定する為には、最低何人を集めなければならないでしょうか?
ただし、この睡眠薬はたった1滴飲んだだけでも効果が現れるとします。また、人を集める、ジュースをグラスに注ぐ等の準備は事前に行えるものとします(開始と同時にジュースを飲むことが可能)。
1,000人を集めて1人1本ずつ飲ませれば、2時間後に眠っている人の飲んだジュースが睡眠薬入りだと特定できますね。「最低何人か」を尋ねられているので、答えは1,000人以下になりそうです。さあ、いったい何人集めれば確実に特定することができるでしょうか。
少し下にスクロールすると答えがあります。
10人
1,000本も調べなければならないのに、たった10人で特定が可能です。どうしてか解説していきましょう。
人によって効果が出る時間が異なるため、睡眠薬入りジュースを特定するには「2時間後にそれを飲んだ人が寝ているか、起きているのか」という情報に頼るしかありません。
また、2時間ちょうどに効果が現れる可能性もあるので、ジュースは開始と同時に飲む必要があります。少ない人数で特定するためには1人が複数のジュースを飲む必要があるため、事前準備として各々のグラスで複数のジュースを混ぜ合わせ、開始と同時にそのグラスを飲み干すことになります。
まずわかりやすくジュースが2本の場合を考えてみましょう。この場合は1人で特定できます。ジュース1を飲まずに、ジュース2を飲みます。Aさんを連れてきてジュース2を飲んでもらうとしましょう。2時間後にAさんが起きていればジュース1、寝ていればジュース2が睡眠薬入りだとわかります。(この場合はAさんは1本しかジュースを飲まないので、事前にグラスで混ぜ合わせる必要はありません。)
次に4本の場合はどうでしょう。この場合は2人いれば特定できます。AさんとBさんを連れてきましょう。わかりやすいように、4本のジュースには「0」〜「3」の番号が書かれたラベルをそれぞれに貼ります(なぜ1〜4じゃないのかは後々解説します)。
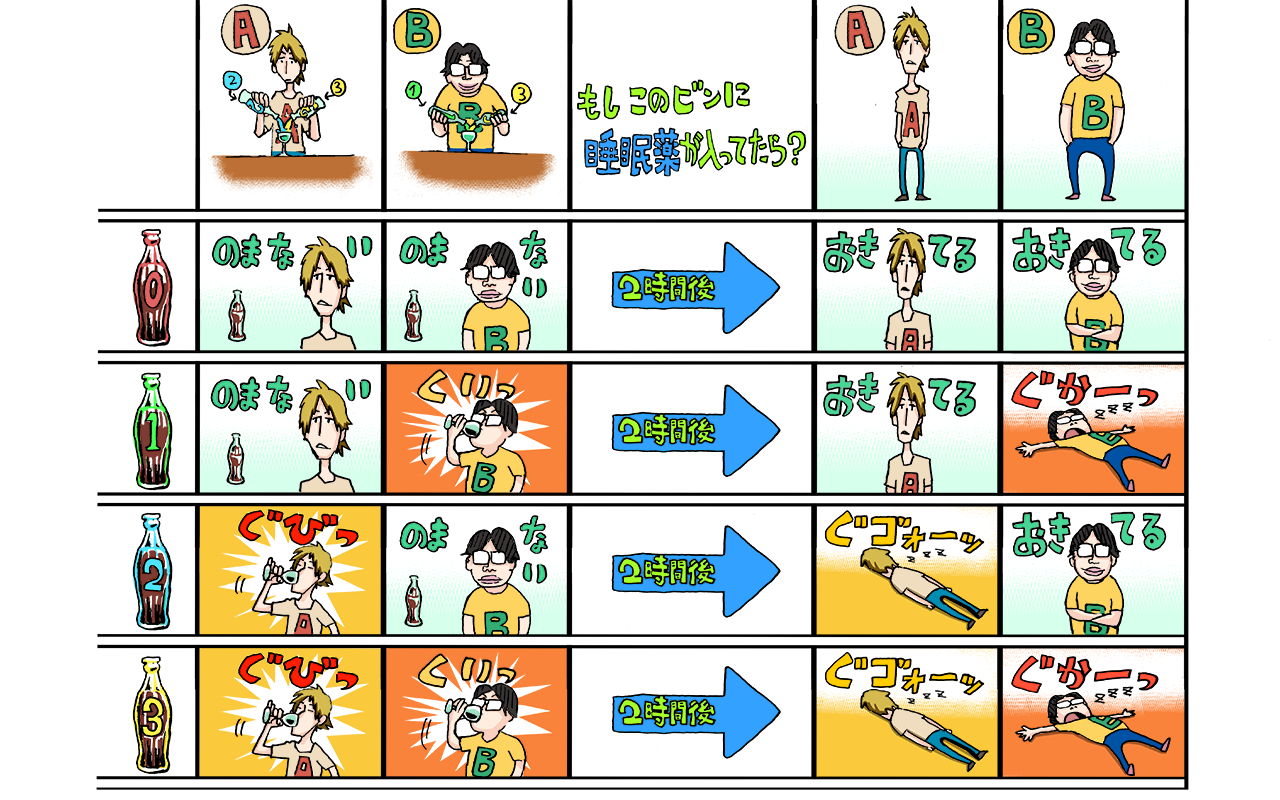
上の図のようにAさんは「2」と「3」のジュースを混ぜ合わせたもの、Bさんは「1」と「3」のジュースを混ぜ合わせたものを開始と同時に飲み干します。Aさん、Bさんそれぞれどのジュースを飲んでどのジュースを飲まないか、を分け2時間後の2人の状態を調べることで2人で4本のジュースを調べることが可能になりました。
それでは8本の場合はどうでしょう? 3人いれば特定することが可能です。Aさん、Bさんに加えてCさんも連れてきましょう。同様にビンに「0」〜「7」まで書かれたラベルをぺたぺたと貼ります。
以下の表では0が「ジュースをグラスに入れない」、1が「ジュースをグラスに入れる」を意味しています。
| ラベルの番号 | A | B | C | 睡眠薬が入っていた場合の2時間後 |
| 0 | 0 | 0 | 0 | 全員起きている |
| 1 | 0 | 0 | 1 | Cが寝る |
| 2 | 0 | 1 | 0 | Bが寝る |
| 3 | 0 | 1 | 1 | B・Cが寝る |
| 4 | 1 | 0 | 0 | Aが寝る |
| 5 | 1 | 0 | 1 | A・Cが寝る |
| 6 | 1 | 1 | 0 | A・Bが寝る |
| 7 | 1 | 1 | 1 | 全員寝る |
2時間後に3人の誰が起きていて誰が寝ているかを調べることで、どのジュースに睡眠薬が入っているかを特定することができました。
ここまでは理解できたでしょうか? 以上を踏まえると、下のような法則が見えてくることがわかります。
それぞれのジュースに対して、飲む・飲まないの2通りの選択が出来るため
- 1人の場合、2の1乗で2本のジュースまで特定可能
- 2人の場合、2の2乗で4本のジュースまで特定可能
- 3人の場合、2の3乗で8本のジュースまで特定可能
となります。
このようにして人数をどんどん増やしていくと、9人の場合512本、10人で1,024本のジュースまで特定することができるので、最低10人いれば1,000本のジュースを調べることが可能となります。
従って、最低10人を集めてくればどのジュースが睡眠薬入りか確実に特定することができます。
これを実際に行う場合、10人それぞれが500本程度ジュースを飲む必要があります。1滴飲んだだけでも効果が現れる強力な睡眠薬でなければ、お腹いっぱいになってしまいますね。なお、スポイト等で1滴を取り出す場合、その平均は0.04ccほどになるそうです。500本でも約20cc程度ですので、開始と同時に飲み干すことは容易ですね。
何故こんな解き方を?
問題の解説は以上になりますが、どうしてこのような考えに至ったのか不思議な人も多いでしょう。本問についてさらに細かく理解を深めていきましょう。
この問題には2進法の考えを用いています。2019年現在では高校1年生の情報の授業で取り扱う内容です。
残念ながら2002年から2010年の間のいわゆる「ゆとり教育」の時代では学習指導要領から外れてしまっていたため、習ったことがない人もいるかもしれません。(かくいう私も学校では習いませんでした・・・!)
軽く2進法についておさらいしましょう。
普段我々は0~9の10個の数字を用いて数を数えます。これは10進法と呼ばれるもので、一番親しみ深い数の数え方ですね。
パソコンを始めとした、ほとんどの電子機器は2進法を用いて動いています。2進法は0と1の2つの数字を用いて数を数えます。
10進法の場合は、1の位、10の位、100の位と桁が増えるごとに10倍ずつ増えますが、2進法の場合は1の位、2の位、4の位、8の位と桁が増えるごとに2倍ずつ増えていきます。
10進法と2進法を書き並べてみますと
| 10進法 | 2進法 |
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
| 11 | 1011 |
| 12 | 1100 |
| 13 | 1101 |
| 14 | 1110 |
| 15 | 1111 |
となります。
この2進法の数字の書き方は上記の解説内で同じものを見ましたね。ビンのラベルを0から始めていたのは、2進法で考えやすくするためだったのです。
10進法で23という数字を023と表しても問題ないように、2進法でも先頭に0をつけて桁数を増やしても数字の持つ意味は変わりません。2進法の表記を10桁まで増やしてみましょう。
| 10進法 | 2進法 |
| 0 | 0000000000 |
| 1 | 0000000001 |
| 2 | 0000000010 |
| ・ | |
| ・ | |
| ・ | |
| 998 | 1111100110 |
| 999 | 1111100111 |
というふうに表すことができました。
それでは改めて2進法を用いて今回の問題を解説していきます。
上記の表のように0000000000〜1111100111(0〜999)の1,000個の数字をビンのラベルに貼り付けます。
Aさん〜Jさんの10人を集めてきて各人に対して、Aさんは10桁目、Bさんは9桁目・・・Jさんは1桁目を担当してもらいます。
そして自分の担当する桁が「1」になっているジュースを自分のグラスに1滴入れます。
例えば10進法で「661」と書かれたラベルは、2進法で「1010010101」ですが、この場合はA,C,F,H,Jさんがそのジュースを飲むことになります。
もし2時間後にこの5人が寝て、他の5人が起きていれば、「1010010101」とラベルに書かれたビンが睡眠薬入りだったと逆算することができるわけです。
「寝る」=「睡眠薬入りジュースを飲んだ」=「睡眠薬入りジュースの担当する桁が1だった」という情報から、2進法を書き出すことで特定することが可能となるんですね。

電源がオンかオフか、電流が流れているか流れていないかなど、2つの情報の組み合わせで表現するときに都合が良いため電子機器には2進法が用いられています。
今回の問題でも1つのジュースに対して、飲む・飲まないの2つの情報があるため、2進法を用いて考えることができました。
2進法について理解を深めたい方はこちらのページを参考にしてみてください。
70年後の世界
2進法における桁数をコンピュータの用語で「bit(ビット)」と呼びます。
先ほどの問題では10人いれば1,024本のジュースまで調べられる、と書きましたがコンピュータ用語では10bitあれば1,024種類の情報を扱うことができる、と言い換えることができます。
コンピュータにはCPUという、パソコンの頭脳に当たる処理装置が搭載されています。このCPUが一度に処理できるサイズはbitを用いて表わされます。任天堂のファミリーコンピュータが8bitだ、というのは耳にしたことがある人も多いのではないでしょうか。8bitですから2の8乗=256種類の情報を一度に扱うことができたわけですね。
現在のパソコンでは64bitのCPUが主流になっています。2の64乗は約1,844京という膨大な数になります。このように情報処理の世界はすさまじいスピードで進歩し続けてきたわけですが、もしこれまでと同じ増加スピードで進歩した場合約70年後に128bitのCPUが登場する計算になります。
ひとつぶの砂をひとつの情報だと考えた時、128bit(2の128乗)は地球100万個分の体積の砂の数と同じ数の情報量ということになります。
スケールが大きすぎてまったく想像がつきませんね・・・。
我々はそんなロマンあふれる時代を生きているのです。
話が大きくなってしまいましたが、次回は身近な猫に関する論理パズルをご紹介していきます!







