
みなさんこんにちは! 林です。

早稲田大学中退。楽器を弾くことと都市伝説が好き。アイリッシュテナーバンジョーという素朴な音色の民族楽器を改造して、パンクロックを演奏するおそらく日本で唯一の人物。最近は水タバコにはまっている。

世にも奇妙な確率!?
ガチャのご利用は計画的に
前回までに不思議な確率の問題を全部で4問紹介してきました。確率のお話は今回が最終回ということで、最後に全世界の数学者が頭を悩ませた有名な難問を紹介します! ぜひ最後までお楽しみください!
変えるべきか? 変えざるべきか?
あなたはTV番組のゲームショーに出演しています。
あなたの前には3つのドアがあります。1つは正解のドアで2つがはずれのドアですが、どれが正解のドアなのか見た目では判別できません。なんの情報も与えられないまま、あなたはドアを1つ選ばなくてはなりません。
あなたが1つのドアを選ぶと、どのドアが正解かを知っている司会者がやってきて、あなたが選ばなかった2つのドアからはずれのドアを1つ開けてみせます。つまり正解のドアはあなたが今選んでいるドアか、残されたもう1つのドアということになります。
ここで司会者があなたに質問をします。「最初に選んだドアから、もう1つのドアに変更しても良いですよ。それとも今のままで良いですか?」
さて、あなたは正解を当てるためにはドアを変えたほうが良いでしょうか?
はずれのドアが1つわかってしまった以上、一方が正解で一方がはずれです。正解に関する情報を何も持っていないのだから、変えても変えなくても確率は1/2のように思えます。はたして、ドアを変えることに意味はあるのでしょうか?
少し下にスクロールすると答えがあります。
「ドアを変えれば正解を選ぶ確率が2倍になるので、変えた方がいい。」
ドアを変えただけで2倍も正解しやすいなんて、にわかには信じられませんね。解説をしていきましょう。
まず解説の便宜上、3つのドアをA、B、Cとして、Aが正解のドアとします(どのドアが正解でも同じ計算をするので結果は変わりません)。
あなたは自分の直感にすごく自信があり、最初選んだドアから絶対変えないとします。この場合は司会者が後から何をしようと関係ありません。最初にAを選ぶと正解、最初にBかCを選ぶとはずれとなるので、正解のドアを選ぶ確率は1/3となります。
反対にあなたは自分の直感に自信がなく、最初選んだドアから必ず変更する場合を考えてみましょう。
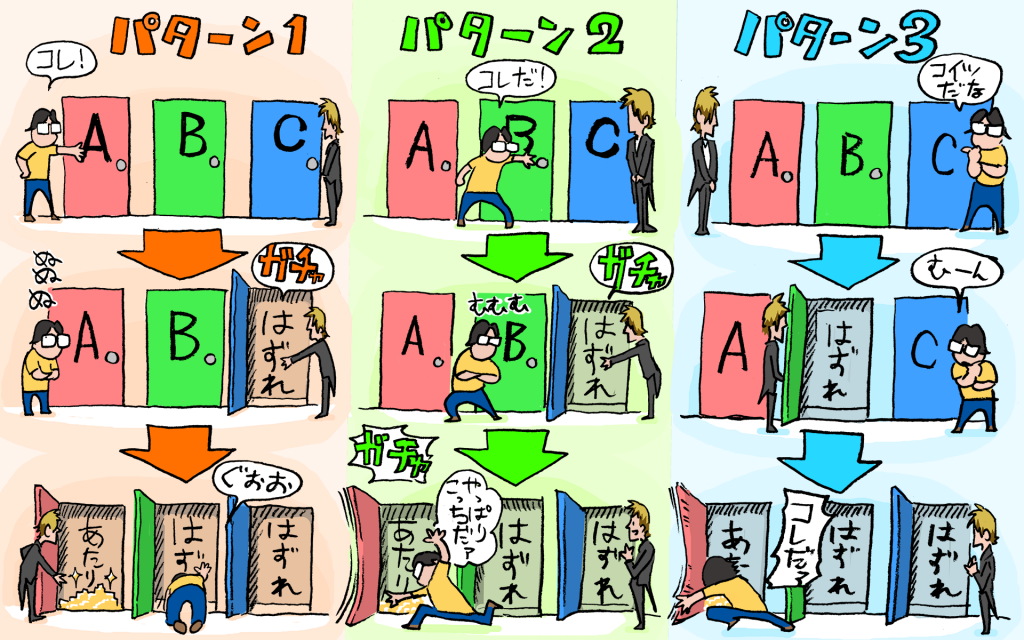
パターン1:A(正解のドア)を最初に選んだ場合、BもCもはずれのドアですね。司会者がどちらを開いてみせようと、Aから変更してしまうと結局はずれのドアを選んでしまいます。
パターン2:B(はずれのドア)を最初に選んだ時はどうでしょう。Aが正解のドアですので、正解を知っている司会者はCのドアを開けてみせます。そのあとあなたはBからAへドアを変更しますので、見事正解することができました。
パターン3:C(はずれのドア)を最初に選んだ場合も同様に、残されたAへ変更するので見事正解となります。
つまり、あなたが選んだドアを必ず変更する場合は、最初にBかCのはずれのドアを選ぶと正解になり、最初にAの正解のドアを選ぶとはずれになります!
よってドアを変更する場合、正解のドアを選ぶ確率は2/3になります。
以上から、ドアを変更しない人が正解する確率は1/3、ドアを変更する人が正解する確率は2/3となり、ドアを変更すれば正解する確率が2倍になるということがわかります。
ややこしくてまだ分からないという方がいるかもしれません。別の方法で解説してみましょう。
ドアの数をドドン!と増やして100個にしてみます。そのうち正解のドアは1つだけです。
あなたは100個のうちからドアを1つ選びます。そうすると正解を知っている司会者が、残された99個のドアから98個のはずれのドアを開けてみせます。さてあなたはドアを変更しますか?
これは当然変更したほうが有利だとわかりますね。残されたドアは、正解を知っている司会者が99個のうちから唯一開かなかったドアなのですから、そのドアが正解のドアの確率が極めて高いように思えます。最初に選んだドアが正解の確率は1/100ですが、変更すれば99/100の確率で正解することができます。
では50個の場合はどうでしょう? これも変更しなければ1/50で正解ですが、変更すれば49/50で正解します。10個の場合はどうでしょう? これも変更すれば9/10で正解します。同様に、ドアが3つの場合でも変更しなければ1/3で正解ですが、変更すれば2/3の確率で正解することができます。
なかなか難しい問題でしたが理解することはできたでしょうか?
モンティ・ホール問題
今回ご紹介したこの問題は数学者でも間違ってしまう、世界を震撼させた問題として有名で、世間一般的に「モンティ・ホール問題(Monty Hall problem)」と呼ばれています。この問題はアメリカのTV番組”Let’s Make a Deal”のゲームが元になっていて(問題の内容自体はほぼ同じで、正解すると新車をゲットできたようです)、この番組の司会者であるモンティ・ホールさんの名前が問題名の由来になっています。
モンティ・ホール問題がここまで有名になるきっかけとなった逸話があります。「世界一IQが高い人物(IQ228)」としてギネスブックに認定されたこともあるマリリン・ボス・サヴァントという人物をご存知でしょうか? マリリンはその知能の高さを活かして、様々なお悩みや質問に回答するという雑誌のコラムを連載していました。
1990年、番組の視聴者からマリリンが連載する雑誌のコラム宛に「ドアを変えるべきなのかどうか」という質問が届きました。マリリンが「ドアを変えると正解の確率が2倍になる」と回答したところ、世界中から反対する意見が10,000通以上届いたそうです。そしてその中には数学の博士号を持っている人物も数多く含まれていました。
その後もマリリンは数回のコラムで再度解説をするものの、彼女への非難はなかなか収まりません。しかし、ある数学者がコンピュータでシミュレーションを行うとマリリンの答えが正しいことがわかり、徐々にこの事態は収束していきました。
モンティ・ホール問題についてはWikipediaにも詳しく記載されていますので、興味のある方はこちらもご覧ください。
さて、いかがだったでしょうか。数学者でさえ間違えてしまうのですから、人間は一度思い込みで信じてしまったことを後から覆すのはなかなか難しいのかもしれません。世の中には自分の直感があてにならないことも沢山あります。何かを決断する際や問題を解決する際に、時間がないなら直感で判断するのも決して悪くはないのですが、時間があるのであれば、立ち止まってじっくり考えてみるといいでしょう。






