
みなさんこんにちは! 林です。

楽器を弾くことと都市伝説が好き。最近はイスラエル音楽にはまっているが、曲名もアーティスト名もヘブライ語なので情報を調べるのに苦戦している。

論理パズルはヤワじゃない
睡眠薬入りジュースを見つけ出せ
前回は1,000本のジュースから睡眠薬入りジュースを見つけ出すという論理パズルを紹介しました!
今回は気まぐれな猫に関する論理パズルを紹介します。
気まぐれな猫
あなたの前に、1~5まで番号の書かれた5つの箱が順番に一列に並んでいます。
この箱の中のどれか一つに気まぐれな猫が隠れています。
あなたは朝に箱を一つだけ開けて猫がいるかどうか調べることができます。猫がいなければその箱を閉めて次の朝を待たなければなりません。しかし猫は夜になると必ず一つ隣の箱にこっそりと移動してしまいます。
さて、あなたは遅くとも何日目までに確実に猫を見つけ出すことができるでしょうか?(確実に見つけ出す為に最も効率の良い行動をとった場合、何日目までに見つけ出せるでしょうか?)
なお、箱をもちあげる、またたびを撒き散らす、ねずみをけしかけるなど、箱を開ける以外の方法で猫がどこにいるかを調べるのはもちろん禁止です。
運が良ければ初日の朝に猫を見つけることができますね。
しかし調べた箱と入れ違いで猫が移動してきたり、延々と二つの箱を行ったり来たりするなど、様々な可能性が考えられます。
そもそも確実に見つけ出すことなど可能かどうかもよく考えないとわかりません。
さあ、どのように調べればこの気まぐれな猫を確実に見つけ出すことができるでしょうか。
少し下にスクロールすると答えがあります。
遅くとも6日目には見つけ出せる。
解説していきましょう。
わかりやすいように箱が3つだけの場合を考えてみましょう。この問題のポイントは「猫は必ず一つ隣の箱に移動する」という点です。
すなわち両端である「1」か「3」の箱に猫が隠れていた場合、夜には必ず「2」の箱に移動してきます。
したがって、まず1日目の朝に「2」の箱を調べ、猫が見つからなかった場合は、猫は「1」か「3」の箱にいることが確定します。夜になると「1」か「3」の箱から「2」の箱へ移動してくるので、2日目の朝も「2」の箱を調べることで2日目までには必ず見つけることができます。
ここまでは理解できたでしょうか?
猫は毎晩「偶数番の箱と奇数番の箱を交互に移動する」ということが重要になってきます。気まぐれに思えた猫ですが、実はこのように限られた動き方しか出来なかったんですね。
それでは今回の問題の解説に入りましょう。
まず1日目の朝に偶数の箱、すなわち「2」か「4」の箱に猫がいると仮定します。
まずは「2」の箱を調べて見ましょう。「2」の箱に猫がいない場合、(仮定が正しければ)猫は「4」の箱にいることになります。そのため猫は夜に「3」か「5」の箱に移動してきます。
2日目の朝は「3」の箱を調べてみましょう。
猫がいない場合は「5」の箱にいることになります。そのため猫は夜に「4」の箱に移動してきます。
当然、3日目の朝は「4」の箱を調べます。
ここで「4」の箱に猫がいない場合、「初日に偶数の箱に猫がいるという仮定」が間違っていたことになります。つまり初日の朝に猫は奇数の箱、「1」・「3」・「5」の箱のどれかにいたことがわかります。
初日の朝に猫が奇数の箱にいた場合、3日目の朝までに猫は2回移動していますので3日目の夜に猫は偶数の箱に移動してきます。
つまり4日目の朝は必ず偶数の箱、「2」か「4」に猫がいることが確定します!!
したがって、1日目の朝から3日目までと全く同じ手順を行いましょう。今度は仮定ではないので必ず見つけ出せます。
4日目の朝に「2」の箱、5日目の朝に「3」の箱、6日目の朝に「4」の箱を調べることで、遅くとも6日目には必ず猫を見つけ出すことができるわけです。
ちなみに1日目の朝に奇数の箱、「1」・「3」・「5」の箱にいると仮定した場合はどうなるでしょう。
「1」・「3」・「5」の箱から移動してきて、2日目の朝は必ず「2」か「4」の箱にいることになるので、「2」か「4」の箱を調べることになります。この時点で解答の1日目と同じ手順を踏むことになりますので、手順が一日増えてしまうため偶数の箱から調べる方がより短い期間で見つけ出すことができます。
今回の解説では「2」→「3」→「4」と調べましたが、「4」→「3」→「2」と調べても手順としては変わりません。
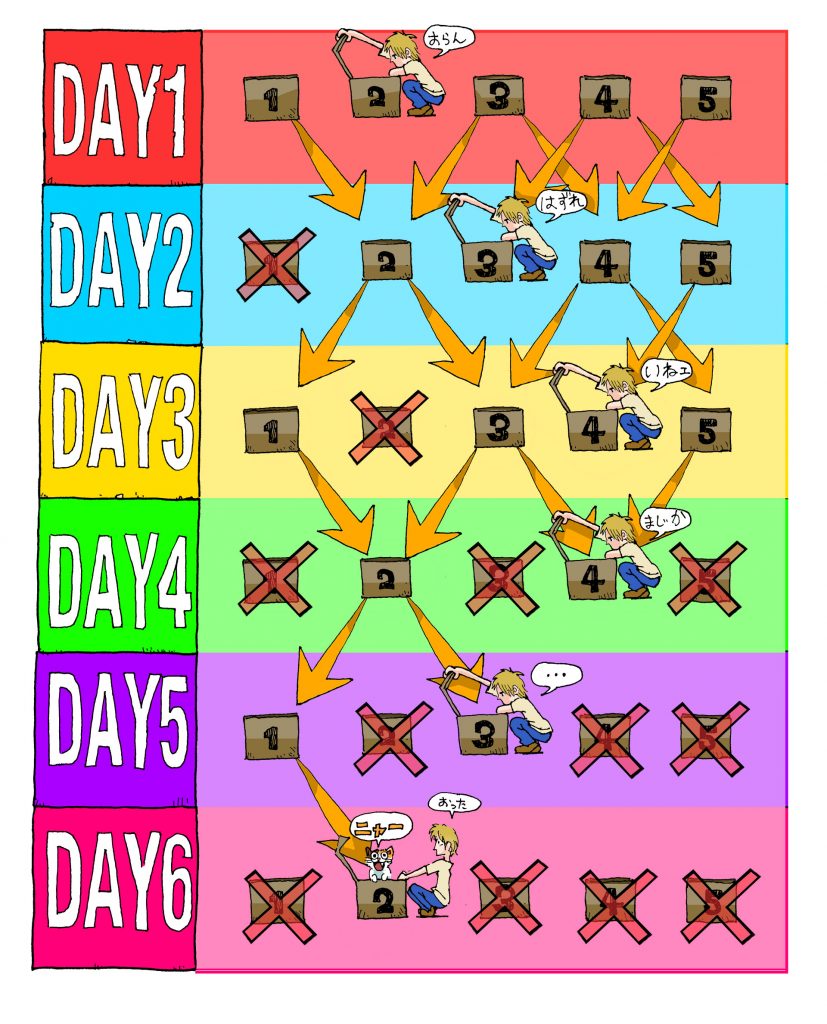
上の図を見てみましょう。
×印は前日の結果を踏まえて、「猫がいる可能性のない箱」を表しています。
例えば、DAY2の「1」と「3」には猫がいないという結果から猫がいる可能性がない為、DAY3の「2」は×印になります。
「2」→「3」→「4」と調べた段階で、DAY4の奇数の箱が全部×印になっているのがわかりますね。4日目の朝には必ず偶数の箱に猫がいることが見て取れると思います。
先ほど解説した通り「2」→「3」→「4」を「4」→「3」→「2」としても問題ないので、図では4日目以降をそのようにして調べました。
したがって猫を探す手順としては
- 「2」→「3」→「4」→「2」→「3」→「4」
- 「2」→「3」→「4」→「4」→「3」→「2」
- 「4」→「3」→「2」→「2」→「3」→「4」
- 「4」→「3」→「2」→「4」→「3」→「2」
の4通りが答えになります。
猫を一般化する
さて、本問の解説は以上になります。なかなか難しく面白い問題でしたね。
しかしこんなもんでは終わらせません、エクストラステージに突入です!
「箱が1,000個の場合遅くとも何日目までに確実に猫を見つけ出すことができるでしょうか?」
1,000個なんて普通に考えていたら日が暮れてしまいますね。何か法則を見つけださなければなりません。数学者になった気持ちで法則を発見しにいきましょう。
上記の解説で、箱が3個の時は2日、5個の時は6日必要だとわかりました。
では箱が7個の場合はどうなるでしょうか?
下記の表を見てみましょう。
「◯」=調べる箱
「□」=猫がいる可能性のある箱
「×」=猫がいる可能性のない箱
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 1日目 | □ | ◯ | □ | □ | □ | □ | □ |
| 2日目 | × | □ | ◯ | □ | □ | □ | □ |
| 3日目 | □ | × | □ | ◯ | □ | □ | □ |
| 4日目 | × | □ | × | □ | ◯ | □ | □ |
| 5日目 | □ | × | □ | × | □ | ◯ | □ |
| 6日目 | × | □ | × | □ | × | ◯ | × |
| 7日目 | □ | × | □ | × | ◯ | × | × |
| 8日目 | × | □ | × | ◯ | × | × | × |
| 9日目 | □ | × | ◯ | × | × | × | × |
| 10日目 | × | ◯ | × | × | × | × | × |
「2」→「3」→「4」に加えて「5」→「6」まで調べることで、1日目に猫が偶数番の箱にいるという仮定が正しいかどうかが判明します。
「2」→・・・→「6」の工程をもう一度繰り返すことになるので、全体としては4日分の工程が増えます。したがって箱が7個の場合は最長10日目に猫を見つけ出すことができます。
視点を変えて箱が4つの場合はどうでしょう?
| 1 | 2 | 3 | 4 | |
| 1日目 | □ | ◯ | □ | □ |
| 2日目 | × | □ | ◯ | □ |
| 3日目 | □ | × | ◯ | × |
| 4日目 | × | ◯ | × | × |
図のように「2」→「3」→「3」→「2」と調べることで最長4日目に見つけ出すことができます。
ここで注意しなければならないのは、これまでのように3日目以降に「2」→「3」と同じ工程を繰り返そうとすると調べる箱の偶奇が入れ替わってしまいます。
図からもわかるように、3日目は(1日目に偶数の箱に猫がいると仮定した場合)奇数の箱に猫がいるので、「2」→「3」→「3」→「2」もしくは「3」→「2」→「2」→「3」が正解となります。
箱が6つの場合はどうでしょう?
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1日目 | □ | ◯ | □ | □ | □ | □ |
| 2日目 | × | □ | ◯ | □ | □ | □ |
| 3日目 | □ | × | □ | ◯ | □ | □ |
| 4日目 | × | □ | × | □ | ◯ | □ |
| 5日目 | □ | × | □ | × | ◯ | × |
| 6日目 | × | □ | × | ◯ | × | × |
| 7日目 | □ | × | ◯ | × | × | × |
| 8日目 | × | ◯ | × | × | × | × |
箱が6つの場合は「2」→「3」に加えて「4」→「5」の工程が増えるので、全体としては4日分の工程が増えます。したがって箱が6個の場合は最長8日で猫を見つけ出すことができます。
さあ、ここまでで何か気がつくことはありませんか?
箱を3個、5個、7個と増やした時、工程が4日ずつ増えていきます。偶数個の場合も同様で4個、6個と増やした時工程が4日ずつ増えていきます。
| 箱の数 | 必ず見つけ出すために必要な日数 |
| 3個 | 2日 |
| 4個 | 4日 |
| 5個 | 6日 |
| 6個 | 8日 |
| 7個 | 10日 |
したがって、箱が一つ増えるごとに調べる日数は2日ずつ増えていくことがわかります。(8個の場合は本当に12日になるかぜひチャレンジしてみてください)
さあ、これまでの情報をまとめて法則を導き出しましょう。以下のようになります。
n個の箱がある場合(n>=3)
| 何日目か | 調べる箱の番号 |
| 1日目 | 「2」 |
| 2日目 | 「3」 |
| 3日目 | 「4」 |
| ・・・ | ・・・ |
| (n-2)日目 | 「n-1」 |
| 何日目か | 調べる箱の番号 |
| 1日目 | 「n-1」 |
| 2日目 | 「n-2」 |
| 3日目 | 「n-3」 |
| ・・・ | ・・・ |
| (n-2)日目 | 「2」 |
手順1→2、もしくは手順2→1で調べることで、遅くとも2×(n-2)日目までに猫を見つけ出すことが可能になります!!
なお、nが奇数の場合には1→1、2→2の調べ方でも可能です。
したがって、1,000個の箱がある場合、2×(1000-2)=1996なので遅くとも1,996日目までに必ず猫を見つけだすことが可能です!(約5年半!!)
このようにあらゆる設定でも成り立つ法則や公式を見つけ出すことを一般化と言います。
一般化は数学や物理学における最終目標の一つであると言えます。
個々の具体的な物事や結果から全体を予想し、その予想が成り立つのであればそれに関するどんなことも導き出すことが可能になります。(今回の問題で言えば、箱が1,000個でも1兆個でもあっという間に答えを出すことが可能になりました。)
りんごが地球に引っ張られている、という具体的な物事をニュートンは一般化して万有引力の法則を発見しました。これにより、地球と他の天体は引き合っている等といった、簡単には観測できない物事まで理解することが可能となったのです。
みなさんにもこの問題を通して、数学の面白さを少しでも感じていただけたら幸いです。
前回に引き続き、2回連続で難問をご紹介してきました。次回はもっと簡単な頭の体操パズルをいくつかご紹介します!







