みなさんこんにちは! 林です。

早稲田大学中退。楽器を弾くことと都市伝説が好き。アイリッシュテナーバンジョーという素朴な音色の民族楽器を改造して、パンクロックを演奏するおそらく日本で唯一の人物。最近は水タバコにはまっている。

世にも奇妙な確率!?
ガチャのご利用は計画的に
前回は直感では信じがたい、不思議な確率の問題を2問ご紹介しました。今回もおもしろい問題を紹介していきます! すぐに答えを見てしまうのではなく、ぜひ自分で考えてみてからお楽しみください。
同じ誕生日は運命?
あなたはあるクラスの担任をしています。生徒の中に同じ誕生日である人のペアが少なくとも1組いる確率が50%を越えるには、クラスの生徒は最低何人いると良いでしょうか?
なお誕生日は完全にランダム(計画出産などは考えない)で、2月29日生まれ(うるう年生まれ)の生徒はいないものとして考えます。
生徒の誰かと誰かが同じ誕生日になる確率。生徒が1人なら0%、366人なら当然100%になりますね。答えは2人〜365人のどこかになりそうです。正確に計算すると大変なのでなんとなくで構いません。このくらいの人数かなと予想してみてください。
自分と同じ誕生日の人って1/365の確率ですから、なかなか出会うことはないですよね。ちなみに調べたところ僕は広瀬香美さんと誕生日が同じようです。さあ、クラスに生徒が何人いればそんなロマンスが起こるのでしょうか。
少し下にスクロールすると答えがあります。
答え
「23人」
予想よりかなり少なかったのではないでしょうか。人間の直感はあてにならないと感じます。解説をしていきましょう。
前回に話題にした「余事象の確率」を使って考えてみましょう。
「同じ誕生日のペアが少なくとも1組いる確率」 = 100% ー 「同じ誕生日のペアが1組もいない確率」
このような式が成り立ちます。すなわち「同じ誕生日のペアが1組もいない確率」を求めれば良いことがわかります。
例えばクラスの生徒が2人の場合、「同じ誕生日のペアが1組もいない確率」は1人目の誕生日はどの日でも問題なく、2人目が1人目と違う誕生日であればいいので、364/365 = 99.7%となります。
クラスの生徒が3人の場合、「同じ誕生日のペアが1組もいない確率」は2人目が1人目と違う誕生日、かつ3人目が他の2人と違う誕生日であればいいので(364/365) × (363/365) = 99.5%となります。少しだけ確率が下がりましたね!
このようにして計算していくと「同じ誕生日のペアが1組もいない確率」は22人目で52.4%、23人目で49.3%になります。
このことから以下の表のようにまとめることができます。
| クラスの人数 | 100% ー 「同じ誕生日のペアが1組もいない確率」 | 「同じ誕生日のペアが少なくとも1組いる確率」 |
| 2人 | 100% ー 99.7% | 0.3% |
| 3人 | 100% ー 99.5% | 0.5% |
| 〜〜〜 | ||
| 22人 | 100% ー 52.4% | 47.6% |
| 23人 | 100% ー 49.3% | 50.7% |
したがって、23人目で「同じ誕生日のペアが少なくとも1組いる確率」が50%を越えることがわかりました!
ちなみに「自分と誰かが同じ誕生日となる確率が50%を越える」にはなんと最低254人いなければなりません!
「自分と誰かが同じ誕生日」ではなく、「クラス内の誰かと誰かが同じ誕生日」とした途端にこんなにも少ない人数で済むのがおもしろいですね。
さて、続いては検査に関する不思議な問題です。
これは本当に不良品?

あなたはとある製品を作る工場で働いています。その工場では1,000個に1個の割合で不良品が出来てしまいます。しかし良品なのか不良品なのか見た目で判断できません。そのため工場では製造レーンの最後で、完成した全ての製品を簡易検査器に通しています。
その検査をおこなうと、不良品は99%の確率で製造レーンから取り除かれます(1%で誤ってしまい、検査器を素通りします)。良品の場合は99%の確率で検査器を素通りします。(1%で誤ってしまい、製造レーンから取り除かれます)。
あなたは製造レーンから「不良品である」と判断され取り除かれた製品群の中から一つを選びます。その製品が不良品である確率は何パーセントでしょうか?
99%と精度が高そうな検査だし、製造レーンから取り除かれた製品群にあるものならほぼ間違いなく不良品に違いない! と思ってしまいますね。さて、どのくらいの確率でしょうか。
少し下にスクロールすると答えがあります。
答え
「約9%」
そんなに低いの!? と驚かれた方も多いでしょう。どうしてそうなるのか、解説をしていきます。
まずわかりやすいようにその日に製造した製品の数を全部で100,000個とします。
1,000個に1個の割合で不良品が発生するので、検査する前の完成した製品の山には不良品100個、良品99,900個が存在しています。不良品100個のうち検査で正しく取り除かれる不良品の数は、99%の確率で抜き出せるので99個となります。一方、良品99,900個のうち製造レーンから誤って不良品として取り除かれてしまう製品(実際は良品)は1%の確率ですので999個となります。
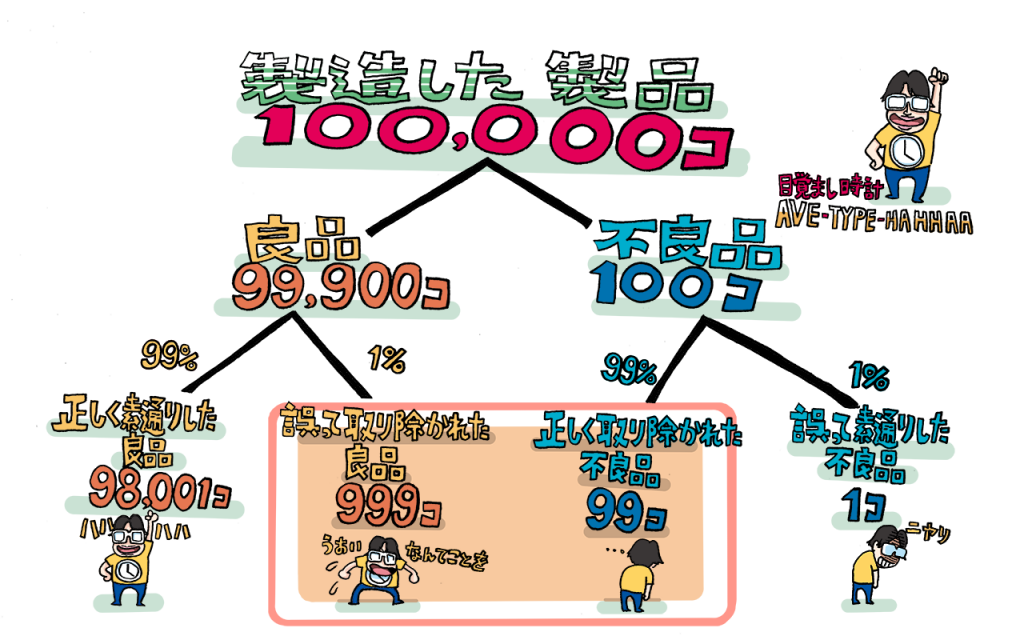
お気付きですか? 誤って取り除かれた良品の数(999個)が、正しく取り除かれた不良品の数(99個)より10倍近く多いんです!
あなたが検査器で不良品と判断され取り除かれた製品群の中から一つの製品を選んだとき、それが実際に不良品である確率は、
(取り除かれた実際の不良品の数)/(取り除かれた製品全体の数)
=99/(99+999)
=99/1098
となります。
これを計算すると、約9.0%が答えになります。
今回の工場の検査だけでなく、健康診断やインフルエンザの検査などにおいても、100%間違いない精度を誇る検査というものはなかなかありません。実は今回取り上げた問題は現代医療では有名な話であり、こういった私たちに身近なところでもひっそりと数学は活躍しています。健康診断や病院での最初の検査による精度が足りない場合は再検査や問診、精密検査を行うことで医者は最終的な診断を下します。
ということで、健康診断の検査でいきなり悪い結果が出たからといっても、本当に病気かどうかはまだ分かりません。ひとまず心を落ち着かせてから病院に行って、じっくりと再検査を受けましょう。
なお、この問題は数学で出てくる「ベイズの定理」の説明でよく使われます(前回の「条件付き確率」をさらに深めた内容になります)。興味がある方は以下のリンク先もご覧いただければ、より一層学びが深まります。
第3回では、全世界の数学者を震撼させた有名な確率の難問をご紹介したいと思います!