
「割る」とは、そもそもいったい何でしょうか? それをはっきりさせておくと、分数のかけざんと割り算をスムーズに理解することができます。
例えば、分数の割り算で分子と分母をひっくりかえしてかけ算をするのはどうして?
といったことも、すんなり理解できるかもしれません。
さて、前回の問題の「1÷1/2はいくつ?」から少し発展してみましょう。

さんすうを読んで解けるようになろう
さんすうは、ことばの言いかえでカンタンになる
【今回の問題】
1/3÷1/2はいくつ?
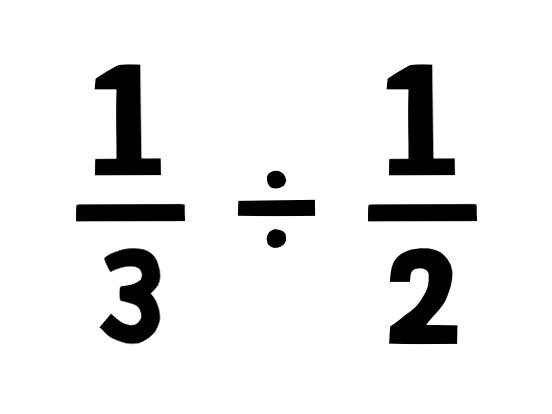
これを翻訳してみると、
「1を3つに分けたものを、1を2つに分けたものに置き換えると、いくつ?」と言えます。
前回の1本のジュースをその半分量のコップに分けると何杯とれるか、は1÷1/2、
その答えが2てのは分かったよね。

はい博士
今回は、1本の1/3量のジュースを、1本の1/2量のコップにとると、どれくらいとれる? ということです。
「割る」ということは、割るものの単位に置き換えるってことなんだ。
ここでいうとビンに入ったジュースをコップ単位に置き換えるとどうなるか?という意味に翻訳することができます。
元々のジュースの量は1/3瓶分、割るものの単位、コップは1/2ジュース瓶分。つまり、1瓶の1/3分入ったジュースを、1瓶の1/2分入るコップに入れたら(コップの単位に置き換えたら)どれくらいまで入りますか?ということです。
[例:1000円札を50円玉に置き換えたら20枚]

ここで大事なのは、頭の中でだいたいどれくらいになるかを想像することです。
1本のビンに3分の1量しかないジュースを、1本の2分の1量が入るコップに入れたら、どれくらい入りそうかな? あふれるかな? あふれないかな?

えーっと、たぶんあふれないです博士!
それを分かることが、すごーく大事です。なぜなら途中で間違いに気付くことができるから。コップの半分だとジュースビンの1/4だし、1/3は1/2より小さいけど1/4よりは大きいし……て考えるのもだいじです。

やってみたら、やっぱりこうなりました。

さて、割り算を分数にする時は、下のようにできることを前回説明したよね。
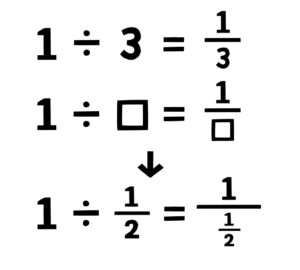
分母と分子は、両方に同じ数をかけていいので、分数をなくすには、今回の問題では何をかけたらいいでしょうか? 下の式を見てみましょう。
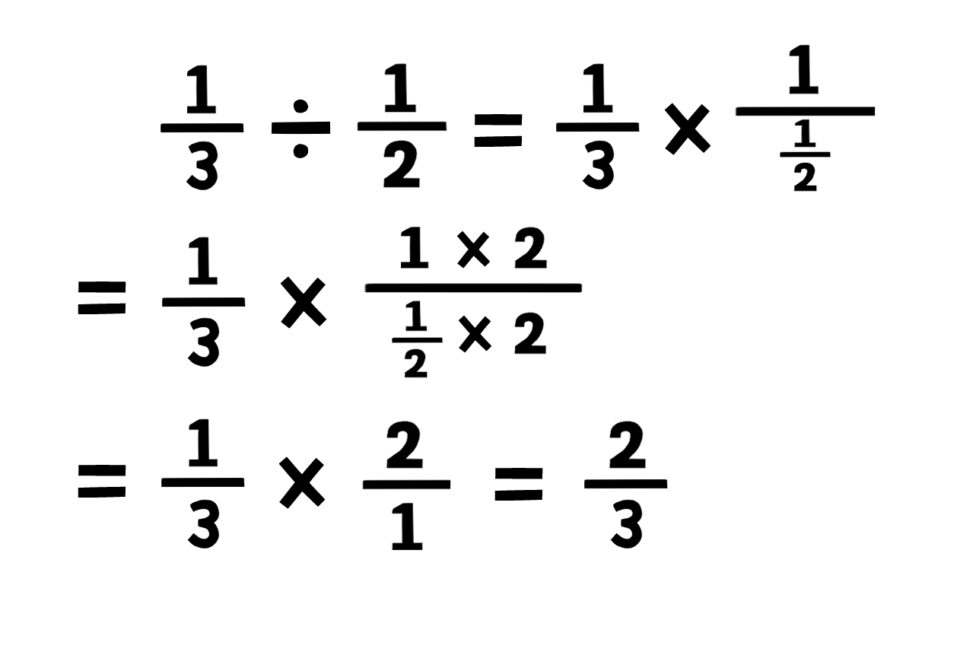
次に、分母と分子に2をかけると
1×2/(3/2)×2
=2/3
になるんだ。
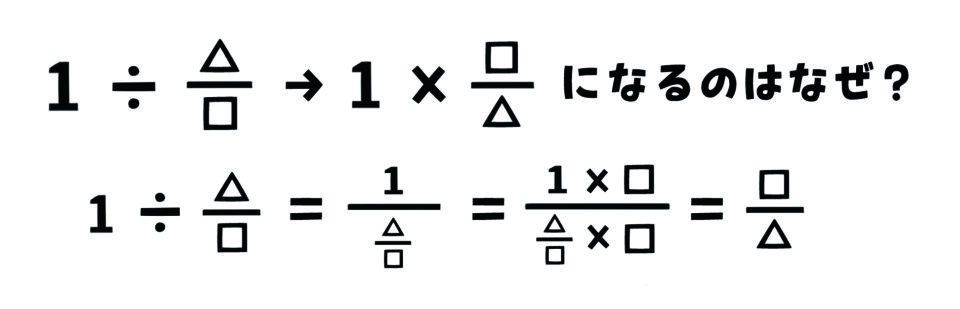
分数の割り算は、上の式のように変化させていくことで、分母と分子が逆になったものを掛けるのと同じであることが証明されるね。普段問題を解くときは、毎回これをやるのはめんどくさいし時間がかかるから、「分数の割り算は分母と分子をひっくり返したものを掛ければいい」という法則を使って解くのだけど、その法則をただ覚えるのではなく、理由を知っておくと理解が深まるよ。
ということで今回のお題、1/3÷1/2を解くと、答えは2/3になるんだけど、「÷1/2」は分母と分子をひっくり返しせばいいとただ覚えるのではなく、ジュースの問題に置き換えてみたり、しっかり通分してみたりして解いていくといろんなことに応用できるようになるよ。

速さと距離
ペンギンハカセはいつ帰ってくる?
CREDIT
クレジット





