
「割る」とは、そもそもいったい何でしょうか? それをはっきりさせておくと、足すや引くはもちろん、掛けるや割るもスムーズにできるようになります。
例えば、分数の割り算で分子と分母をひっくりかえしてかけ算をするのはどうして?
といったことも、すんなり理解できるかもしれません。

さんすうを読んで解けるようになろう
さんすうは、ことばの言いかえでカンタンになる
【本日の問題】

この問題を解く前に、もう少し基本的なことをしっかり理解しておくことが大切です。
1÷2 をまずは考えてみましょう。

「1を2で割ることは想像ができます」
「でも、1を1/2で割ることは想像しにくいです」
そうだね。1/2で割るってなんだ!?ってなるよね。でも1を2で割ることも、1を1/2で割ることも、現実の話では、どっちもよくあることなのです。
現実にあるものに置き換えることによって実感が持てるので、理解が深まるようになるので、問題を現実の話に置き換えて考えることはとても重要な作業です。
たとえば、4÷2=2の場合。
「4個のりんごを2人で均等に分けたらひとりあたり何個もらえるでしょうか」
という問題に置き換えることができます。答えはわかるかな?

「2個です」
そうだね。では次に1÷2を例えると、
「1つのホールケーキを2人で均等に分けたら、1人あたりケーキ何個分もらえますか」
と言い換えることができますが、これはわかるかな?

「1/2個分です」
そうだね。では次の問題はどうかな。
1÷1/2、これを現実の話に翻訳するとこんな問題ができます。
「1本のジュースをその半分量がとれるコップに分けるとコップ何杯分ですか?」

これが1÷1/2の考えかたです。
答えはどうなりますか?

「あ、2杯です!」
正解。
「割る」というのは、「元の単位から割るものの単位に置き換えること」と翻訳することができます。
一見すると「おや、増えた?」ということも起こるけれど、実際には増えていませんね。
単位が変わっただけなのを確認してください。今回はジュースの瓶1本→コップ2杯と「本」から「杯」に置き換わっています。
1÷1/2=2を別のアプローチで考えてみましょう。
1÷2と1/2はただ表記が違うだけで同じですね。
1÷2は1/2と書いてOK。
日本語にすると、1割る2は2分の1と書いてもよい。
ちなみに1÷1/2をこう書くこともできます。
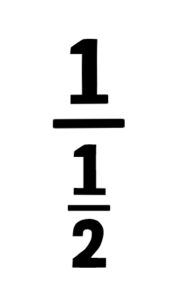
数式だけで解くには、通分の知識が必要ですね。
ちょっと話しが横道にそれるけど、通分はできるかな?
2/4→1/2、と割ったり
2/3→4/6、とかけたり
分母と分子に同じ数をかけたり割ったりしてもよいというルール、これが通分です。
1/(1/2)
これを通分したらどうなるでしょうか。
分子と分母にそれぞれ2をかけてみましょう。
1×2/(1/2)×2=2/1となるね。つまりこうなります。
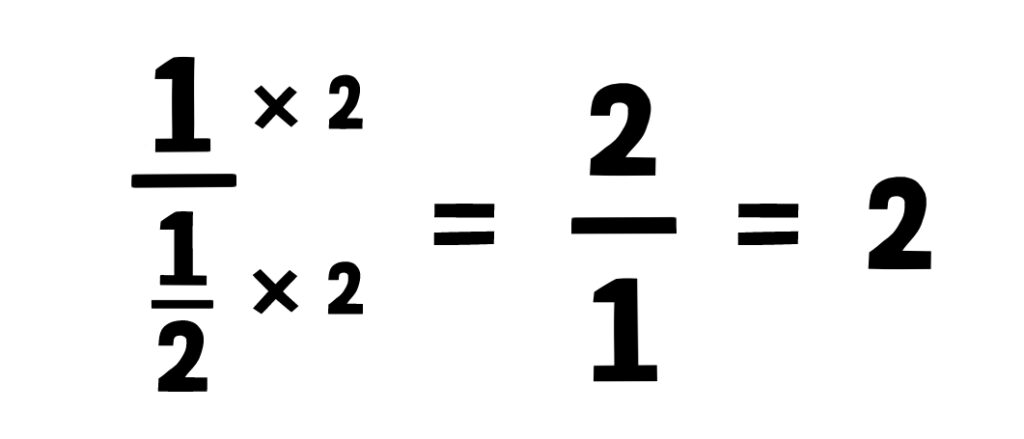

答えは2!
そうだね、これが 1本のジュースを、その1/2量とれるコップに移すとしたら、コップ何杯分とれますか? の数式バージョンです。
ここまで分かったら分数と分数の割り算はお手の物だよ。
続きはまた来週!

割るってなあに?
割り算と分数を理解しよう②
CREDIT
クレジット





