
みなさん、さんすうは好きですか? 「すき!」と答えられる子はそんなにいなそうですね。おとなでも「好き!」といえるおとなは少ないものです。さて、もうすぐたのしい夏休み。この期間をつかって、ペンギンハカセがさんすうを読みながら解説していくコラムです。夏休み明けにさんすうが得意科目になってくれるとうれしいです。

ハカセ、さんすうはどうしてむずかしいの?
バーンと図があって 「〇〇を求めよ 」と言われると、「う…」となってしまうかもしれないけど、すぐに答えを出そうとしなければ、もう少し構えなくてすむよ。
問題文を見てむずかしいと感じたなら、カンタンになるように自分で変えていけばいいのさ。ポイントは、「すぐ答えをだそうとしないこと」だね。

図とか出てくると、問題を読む気もなくなります。
それはやっぱりすぐに答えを出そうとしてしまっているね。問題文をいきなり全部理解する必要はないんだ。問題文をとりあえず最初から最後までしっかり見てみることが大事だよ。図ならどんな図なのかをしっかり観察することだね。そこからこの問題を解くにはどうしていけばいいかをかんがえていくんだ。具体的には自分がわかりやすい、解きやすいように問題自体を変化させていくの。それをここでは「翻訳(ほんやく)」ということにしよう。いっぺんに解こうとするとむずかしいけど、一つ一つ翻訳しながら進めていくと、おどろくほどカンタンな問題になったりするんだよ。
さんすうは、だいたいが言葉の置き換えでカンタンになるんだ。いかに翻訳できるか、ただそれだけなんですよ。
たとえば、こちらの例文を見てみましょう。
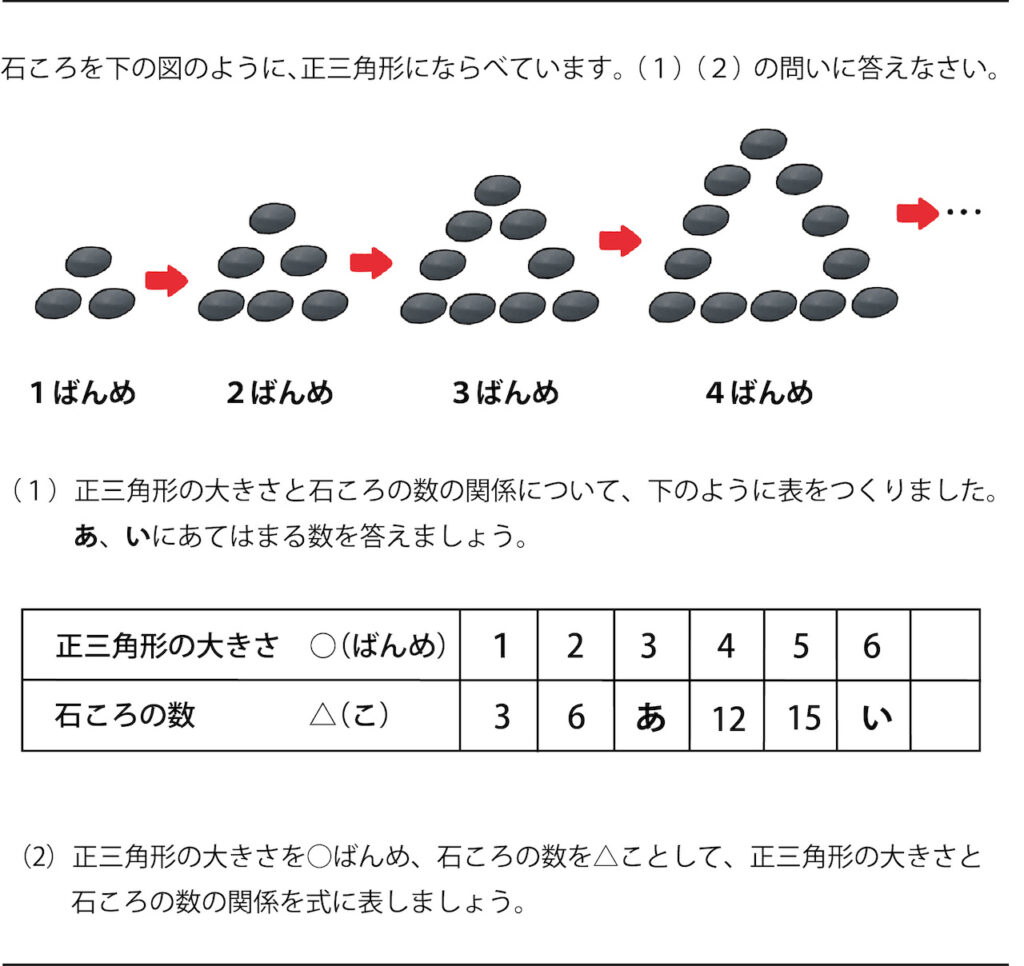
いきなり解こうとすると、むずかしくて混乱しそうですね。
まずは問題の特徴を抜き出してみよう。
※だぶってもいいので特徴を書いてみましょう

「正三角形」
「だんだん大きくなる」
「石ころの数はどうやってふえていくのかな」
「3番目と6番目の石ころの数を答える」
「〇番目の石ころの数は△個」
「〇が増えると△はどのようにふえるか」
うん、そんなところでしょうか。
ではこれをもとに、問題を解いていってみましょう。
「3番目の石ころの数を答える」
これは図にも書いてあるので、数えれば解けちゃいますね。

ハカセ、9です!
では6番目の石ころの数はいくつでしょうか。
これは図にはありません。実際に5番目、6番目と書いてみてもいいかもしれませんが、もし、これが、100番目だったらちょっと書くのはむずかしくなりますね。だから、ここは無理やり書くのではなく、番目がふえると、石ころはどのように増えていくかの法則を見つけていくことにしましょう。
ここで図をもう一度みてみましょう。番目が増えるとどのように変化しているかを考えます。
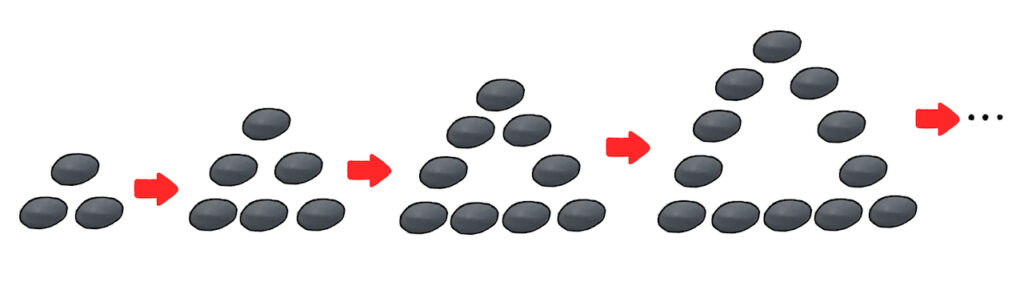
「大きくなっていく」
「正三角形のまま」
というのが見て取れると思います。
そんな特徴は当たり前だよと思うかもしれないけど、この特徴を自分自身で認識することがとても重要なのです。
それを認識することによって、もともとの問題から、
「番目が増えると正三角形がおおきくなる。そのときの石ころの数はどのようにふえていくの?」
という問題に翻訳することができます。
翻訳ができたらもうけもの。それをどんどんくりかえしていくことによって、問題をカンタンにすることができるのです。
いろいろ、言い換えてみましょう。
「正三角形が大きくなるときは、実際どこが増えている?」
「三角形は角が三つの図形」
→「三角形は角が4つでも5つでもダメ、3つに限る」
→「角はかならず3つ」
というルールを翻訳することによって、こんな仮説が立てられます。
「角が増えることはないから、三角形が大きくなるとしたら、辺にあたる部分だろう」
これをもとに図を見直してみましょう。


はい、ハカセ。どうやら、番目が増えるごとに、1辺の石ころの数が1個ずつ増えていっているように見えます。
その通り。その発見がとても重要だよ。
これをもとに、図を日本語で表してみるとしよう。
1番目の三角形→ 1辺に増えた石ころの数は0→ 3辺で増えた石ころの数は0
2番目の三角形→ 1辺に増えた石ころの数は1→ 3辺で増えた石ころの数は3
3番目の三角形→ 1辺に増えた石ころの数は2→ 3辺で増えた石ころの数は6
4番目の三角形→ 1辺に増えた石ころの数は3→ 3辺で増えた石ころの数は9
※3角形なので辺は3つある。正三角形なので全部同じ長さ=石ころの数になる
これに角の石ころを足した数が三角形の石ころの数になるね
1番目の三角形 → 角の石ころ3個と、辺の石ころの合計数0個で3個
2番目の三角形 → 角の石ころ3個と、辺の石ころの合計数3個で6個
3番目の三角形 → 角の石ころ3個と、辺の石ころの合計数6個で9個
4番目の三角形 → 角の石ころ3個と、辺の石ころの合計数9個で12個
あらあら、なんか法則が出てきたようなきがしませんか。
1番目=3+0
2番目=3+1×3
3番目=3+2×3
4番目=3+3×3

元の石ころの数(3個)+増えた石ころの数×3辺だ!
これをまとめると
1番目=3個
2番目=6個
3番目=9個
4番目=12個
〇番目=△個
この〇と△の関係は、〇×3が△と同じになりますね。
だから、
〇×3=△・・・⑵の答え
これができてしまえば、5番目だろうが6番目だろうが100番目だろうが怖くないですね
6番目は
6×3=18個・・・⑴の答え
方程式ができる人の場合は以下の通り
△=3+(〇-1)×3
△=3+3〇-3
△=3×〇
となります。
さんすうで「ひらめく」ことは、いきなりはむずかしいから、そのひらめきを得るためにも問題を翻訳してカンタンにしていく作業がたいせつです。
ひらめくためには分析、つまり観察が必要なのだ。
これがとても重要で、自分がひらめくための作業をしましょう、というのが「読むさんすう」の本題でもあります。 記号とか数式だらけだとひらめきにくいから、それを日本語に翻訳していくことで、さんすうを理解していくってことだね。
さて、小学生がつまずきやすい単元として「割算」がありますが、次回は「割算」を読み解いていきます。

割るってなあに?
割り算と分数を理解しよう①
CREDIT
クレジット





