
夏休みが終わってしまいました。しかも秋まで連れてきた9月ですが、張り切って算数先生と「さんすう」を楽しみましょう。さて、本日は「速さと距離」についてです。こちらも小学生は苦手な子は苦手な問題ですが、生活に根付いた内容ですから、しっかりおさえておきたいものです。

さんすうを読んで解けるようになろう
さんすうは、ことばの言いかえでカンタンになる
【今回の問題】
ペンギン村から南極地点まで行くために、ペンギンハカセは秒速30mで走る長さ50mの列車に乗ります。途中で700メートルあるトンネルがあります。列車がトンネルに入り始めて、出るまでにかかる時間を答えましょう。
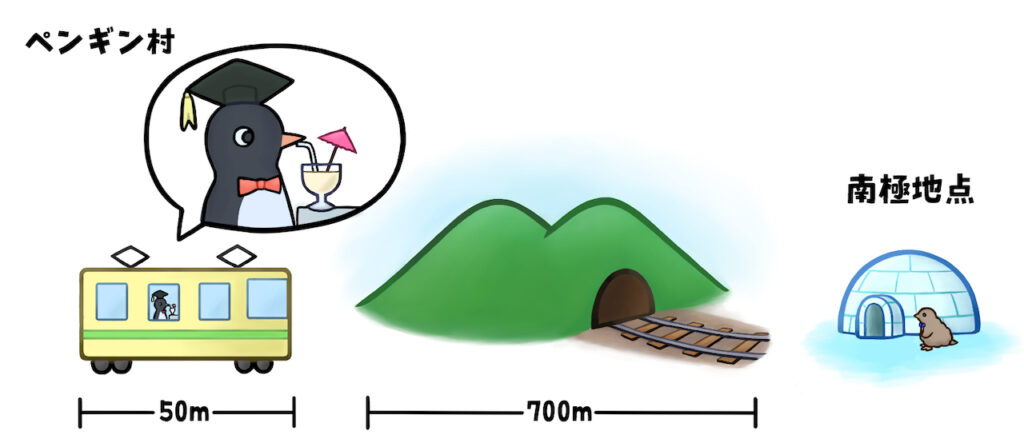
距離と速さと時間に関係する問題は、なんだか複雑で難しく思えますが、
実はポイントをしっかり押さえておけば、カンタンに解くことができるようになります。
そのポイントは大きく分けて2つあります。
1つは、公式をしっかり理解して、覚えること。


ハカセ、覚えられません
この三つの公式が基本なのですが、実はこのうちのどれか1つだけ覚えておけばそれでOKなのです。
ここでは、一番上の、距離=速さ×時間、
日本語にすると「距離は速さに時間をかけたもの」
をベースにしましょう。
中学校で習う方程式には両辺に同じものを掛けても割ってもいいというルールがあります。
方程式というのは簡単にいうとイコール(=)でつながれた数式のことです。
つまり距離=速さ×時間 は方程式ということになります。
方程式は左辺と右辺に分かれます。
左辺(距離)=右辺(速さ×時間)
ここで知っとくとお得なことは、
「左辺と右辺に同じものを掛けても割ってもいい(ちなみに足しても引いてもいいです)」
ということです。
このルールを使えば、距離と速さと時間はお手の物です。
距離=速さ×時間
の両辺(左辺と右辺)を速さで割ってみましょう。
距離÷速さ=速さ×時間÷速さ
(右辺)=速さ÷速さ×時間→速さ/速さ×時間=1×時間
※速さを速さで割るとちょうど割り切れて1になることがポイントです。
となり、
距離÷速さ=時間
という式が導きだせます。
同様に
距離=速さ×時間の両辺を時間で割ったら
距離÷時間=速さ×時間÷時間
距離÷時間=速さ×時間/時間=速さ×1
距離÷時間=速さ
という式に導けますね。

時間と速さと距離の関係は、1つだけ覚えておけばあとは自力で計算できるんだ!
おそらく一番イメージわきやすいのは距離=速さ×時間だと思うので、これを覚えるようにしてみましょう。
「距離は、進むスピードとかかる時間で決まる」
という意味ですね。
時速10キロで1時間進むと10キロ進みます。
時速10キロで2時間進むと20キロ進みます。
といったかんじです。
実際の事がらに置き換えてイメージできるようにすることが重要です。
距離=速さ×時間
時間を求めたかったら、両辺を速さで割って、時間=距離÷速さ
速さを求めたかったら、両辺を時間で割って、速さ=距離÷時間
とすぐに出せますね。
距離は、速さと時間を掛けたものってことをしっかり覚えておけばあとはちょっとした計算でいいってことです。
距離と速さと時間に関係する問題を解く上で重要なポイントその2は、
距離と速さと時間、この3つの要素のうち、2つがわかっていれば答えがでるということを理解しておくことです。
距離と速さと時間、このうち1つしかわかってない場合は問題は絶対に解けません。
裏を返して言えば、この手の問題は必ず、三つの要素のうち2つが事前にわかるようにできているということなんです。
ここで問題を見返してみましょう。
ペンギン村から南極地点まで行くために、さんすう先生は秒速30mで走る長さ50mの列車に乗ります。途中で700メートルあるトンネルがあります。列車がトンネルに入り始めて、列車が完全に出るまでにかかる時間を答えましょう。
ちょっと考えてみましょう。列車の先頭がトンネルに入ってから、列車の最後方がトンネルを抜けるまでが条件であることに気を付ければ、あとは公式に当てはめるだけで解けますね。
距離=速さ×時間
を変形して
時間=距離÷速さにしましょう。

で答えは25秒。
3つのうちわかってる2つはなにか、わかってない1つは何かを考える癖をつけましょう。
そうすると応用問題も解けるようになっていきます。

どうして算数は苦手な人が多いの?
ペンギンハカセの三者面談
CREDIT
クレジット





